精英中考网消息：2017年山东省济南市中考已经结束，六月，又有一批新的考生参加2018中考，为了帮助广大考生更好的复习备考，小编收集整理了2017济南中考各科试题及参考答案，供广大考生参考，下面是2017济南中考数学试题试卷及答案

27．(2017济南，27，9分)

某学习小组的学生在学习中遇到了下面的问题：

如图1，在△ABC和△ADE中，∠ACB＝∠AED＝90°，∠CAB＝∠EAD＝60°，点E，A，C在同一条直线上，连接BD，点F是BD的中点，连接EF，CF，试判断△CEF的形状并说明理由．

问题探究：

（1）小婷同学提出解题思路：先探究△CEF的两条边是否相等，如EF＝CF，以下是她的证明过程

证明：延长线段EF交CB的延长线于点G． ∵F是BD的中点， ∴BF＝DF. ∵∠ACB＝∠AED＝90°， ∴ED∥CG.

∴∠BGF＝∠DEF. 又∵∠BFG＝∠DFE， ∴△BGF≌△DEF(       ). ∴EF＝FG. ∴CF＝EF＝EG.

请根据以上证明过程，解答下列两个问题：

①在图1中作出证明中所描述的辅助线；

②在证明的括号中填写理由（请在SAS，ASA，AAS，SSS中选择）．

（2）在（1）的探究结论的基础上，请你帮助小婷求出∠CEF的度数，并判断△CEF的形状．

问题拓展：

（3）如图2，当△ADE绕点A逆时针旋转某个角度时，连接CE，延长DE交BC的延长线于点P，其他条件不变，判断△CEF的形状并给出证明．

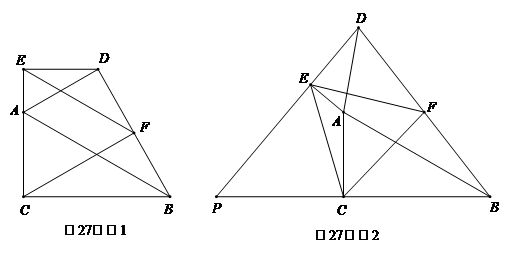
【解】（1）①证明中所叙述的辅助线如下图所示：

②证明的括号中的理由是：AAS.

（2）△CEF是等边三角形．证明如下：

设AE＝a，AC＝b，则AD＝2a，AB＝2b，DE＝a，BC＝b，CE＝a＋b.

∵△BGF≌△DEF,∴BG＝DE＝a.∴CG＝BC＋BG＝(a＋b)．

∵＝＝，＝，∴＝.

又∵∠ACB＝∠ECG，∴△ACE∽△ECG.

∴∠CEF＝∠CAB＝60°.

又∵CF＝EF(已证)，

     ∴△CEF是等边三角形．

（3）△CEF是等边三角形．

证明方法一：

如答案图2，过点B作BN∥DE，交EF的延长线于点N，连接CN，则∠DEF＝∠FNB.

又∵DF＝BF，∠DFE＝∠BFN，∴△DEF≌△BNF．∴BN＝DE，EF＝FN．

设AC＝a,AE＝b,则BC＝a,DE＝b．

∵∠AEP＝∠ACP＝90°，∴∠P＋∠EAC＝180°．

∵DP∥BN，∴∠P＋∠CBN＝180°．∴∠CBN＝∠EAC．

在△AEC和△BNC中，

∵＝＝＝,∠CBN＝∠EAC,

∴△AEC∽△BNC.∴∠ECA＝∠NCB.∴∠ECN＝90°.

又∵EF＝FN，

∴CF＝EN＝EF.

又∵∠CEF＝60°,

∴△CEF是等边三角形．

证明方法二：

如答案图3，取AB的中点M，并连接CM，FM，则CM＝AB＝AC.

又∵∠CAM＝60°,∴△ACM是等边三角形.

∴∠ACM＝∠AMC＝60°.

∵AM＝BM,DF＝BF,∴MF是△ABD的中位线.∴MF＝AD＝AE且MF∥AD.

∴∠DAB＋∠AMF＝180°.

∴∠DAB＋∠AMF＋∠AMC＝180°＋60°＝240°.

即∠DAB＋∠CMF＝180°＋60°＝240°.

又∵∠CAE＋∠DAB＝360°－∠DAE－∠BAC＝360°－60°－60＝240°，

∴∠DAB＋∠CMF＝∠CAE＋∠DAB

∴∠CMF＝∠CAE.

又∵CM＝AC,MF＝AE，

∴△CAE≌△CMF.∴CE＝CF,∠ECA＝∠FCM.

又∵∠ACM＝∠ACF＋∠FCM＝60°,

∴∠ACF＋∠ECA＝60°.即∠ECF＝60°.

又∵CE＝CF,

∴△CEF是等边三角形．

上一页  [1] [2] [3] [4] [5] [6] 下一页

中考信息不断变化,精英中考网www.91post.com提供的中考资讯、成绩查询、分数线信息仅供参考，具体以相关教育部门的信息为准！