精英中考网消息：2017年山东省济南市中考已经结束，六月，又有一批新的考生参加2018中考，为了帮助广大考生更好的复习备考，小编收集整理了2017济南中考各科试题及参考答案，供广大考生参考，下面是2017济南中考数学试题试卷及答案

28．（2017济南数学9分)

如图1，矩形OABC的顶点A，C的坐标分别为(4，0)，(0，6)，直线AD交BC于点D，tan∠OAD＝2，抛物线M1：y＝ax2＋bx(a≠0)过A，D两点．

（1）求点D的坐标和抛物线M1的表达式；

（2）点P是抛物线M1对称轴上一动点，当∠CPA＝90°时，求所有符合条件的点P的坐标；

（3）如图2，点E（0，4），连接AE，将抛物线M1的图象向下平移m(m＞0)个单位得到抛物线M2．

①设点D平移后的对应点为点D′，当点D′恰好在直线AE上时，求m的值；

②当1≤x≤m(m＞1)时，若抛物线M2与直线AE有两个交点，求m的取值范围．

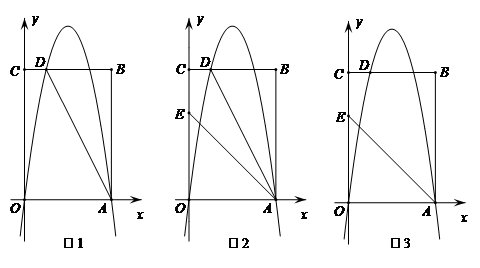
【解】

（1）过点D作DF⊥OA于点F，则DF＝6.

∵tan∠OAD＝＝2，∴AF＝3.∴OF＝1.

∴D(1，6).

把A(4，0)，D(1，6)分别代入 y＝ax2＋bx(a≠0)，得

.解得.

∴抛物线M1的表达式为：y＝－2x2＋8x.

(2)连接AC，则AC＝＝2.

∵y＝－2x2＋8x＝－2(x－2)2＋8，

∴抛物线M1的对称轴是直线x＝2．

设直线x＝2交OA于点N，则N(2，0).

以AC为半径作⊙M，交直线x＝2于P1、P2两点，分别连接P1C、P1A、P2C、P2A，则点P1、P2两点就是符合题意的点，且这两点的横坐标都是2．

∵点M是AC的中点，∴点M（2,3）．∴MN＝2.

∵P1M是Rt△CP1A的斜边上的中线，∴P1M＝AC＝.

∴P1N＝MN＋P1M＝3＋.

∴点P1(2，3＋).

同理可得点P2(2，3－).

（3）由A(4，0)，点E（0，4）可得直线AE的解析式为y＝－x＋4.

①点D(1，6)平移后的对应点为点D′(1，6－m)，

∵点D′恰好在直线AE上

∴6－m＝－1＋4.

解得m＝3.

∴D′(1，3)，m＝3.

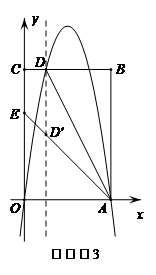
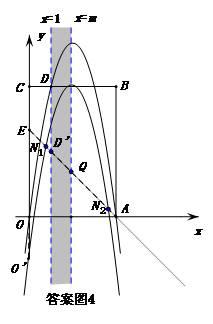
②如答案图4，作直线x＝1,它与直线AE的交点就是点D′(1，3).作直线x＝m交直线AE于点Q(m，－m＋4).

设抛物线M2的解析式为y＝－2x2＋8x－m．

若要直线AE与抛物线M2有两个交点N1、N2，则关于x的一元二次方程－2x2＋8x－m＝－x＋4有两个不相等的实数根，

将该方程整理，得2x2＋9x＋m＋4＝0.

由△＝92－4×2(m＋4)＞0，

解得m＜.

又∵m＞1，

∴1＜m＜…………………………………………………………………………①

∵1≤x≤m(m＞1)，

∴抛物线M2与直线AE有两个交点N1、N2要在直线x＝1与直线x＝m所夹的区域内（含左、右边界）.

当点N1与点D′(1，3)重合时，把D′(1，3)的坐标代入y＝－2x2＋8x－m，可得m＝3.

∴m≥3…………………………………………………………………………②

当点N2与点Q(m，－m＋4)重合时，把点Q(m，－m＋4)的坐标代入y＝－2x2＋8x－m，可得

－m＋4＝－2m2＋8m－m.解得m1＝2＋，m2＝2－（不合题意，舍去）.

∴m≥2＋…………………………………………………………………………③

由①、②、③可得符合题意的m的取值范围为：

2＋≤m＜．

上一页  [1] [2] [3] [4] [5] [6] 

中考信息不断变化,精英中考网www.91post.com提供的中考资讯、成绩查询、分数线信息仅供参考，具体以相关教育部门的信息为准！